Rilasciata la nuova versione IDEA StatiCa 23.1 ►►►Leggi le Release…
Saremo presenti al GEOFLUID 2023 di PIACENZA dal 13 al 16 Settembre. Padiglione 1 - Corsia A - STAND 41 Geofluid è la più…
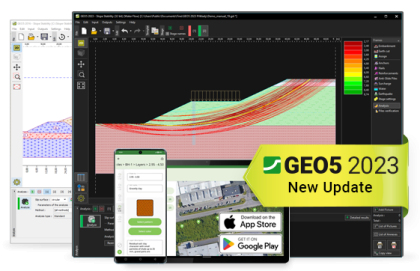
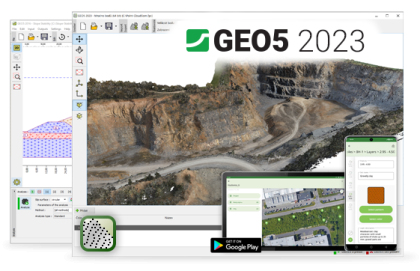
App Mobile per Data Collector GEO5 Data Collector - Applicazione per dispositivi mobile (iOS, Android) per la raccolta dei dati durante…
Saremo presenti al SED 2023 che si terrà a CASERTA dall'11 al 13 Maggio. Eiseko ti permetterà di partecipare a…
Disponibile il plugin della Stacec per esportare nodi da FaTa Next verso IDEA StatiCa Connection. .dividea{ …
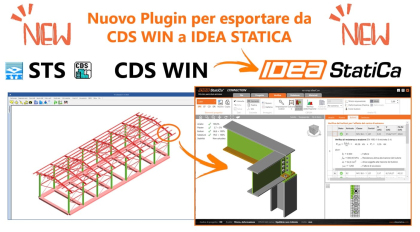
Disponibile il plugin della NextFEM per esportare nodi e membrature da CDS Win (STS) verso IDEA StatiCa Connection e Member: è…
15/11/2022 Nuova Edizione GEO5 2023 GEO5 Edizione 2023 - Nuove funzionalità e Nuovi Programmi Nuova applicazione Mobile GEO5 Data…
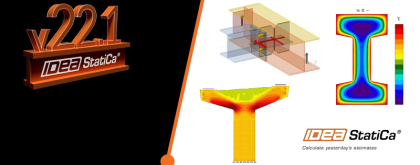
Rilasciata la nuova versione IDEA StatiCa 22.1 ►►►Leggi la Release…

 CYPE Architecture: Software Bim gratuito
CYPE Architecture: Software Bim gratuito